导读:本文介绍了由浙江大学肖刚、骆仲泱、倪明江团队提出的一种以蜂窝陶瓷作为高温固体显热储热材料的储热系统。通过搭建蜂窝陶瓷储热系统的试验系统,进行储热性能试验研究;在试验的基础上,总结了蜂窝陶瓷常用的计算数值模型,并通过试验验证了模型的准确性。在试验中,储热2小时的热量可提供约30分钟的有效放热时间,储热系统热效率约为66%。模拟结果和试验值的吻合性较好,在储热期结束时,两者偏差在5%以内。而在放热期,两者偏差逐渐明显,出口附近温差约为20℃。当通道直径减少或者壁厚增加时,有效放热时间(出口空气温度>600℃)可达8小时。当同时优化蜂窝陶瓷蓄热体的几何参数和空气流量时,出口空气温度在储热期内上升缓慢,在8小时放热期内温度由980℃下降至790℃,储热系统的热效率可达90%。
本文提出了一种适用于太阳能热发电的蜂窝陶瓷储热系统,建立储热系统数值模型并通过试验对其进行验证。在储热期结束时,模型与实验结果偏差在5%以内,模拟结果与试验值吻合较好。数值模型用来分析几何参数以及热物理参数和空气流量对储热系统的影响。当传热较少时温度下降更快并且在放热阶段降至更低的温度。系统储热能力随着容积比热容的增加而提高。对于大通道直径和较薄壁厚的储热系统,出口温度在储热阶段上升迅速,在放热阶段急剧下降。
1.简介
在太阳能热发电系统中,储热系统有着重要作用及意义,在太阳辐射充足时蓄积部分热量;在太阳辐射不足或者没有太阳辐射时可利用蓄积的热量继续发电。在太阳能热发电系统中,运用储热技术可以降低发电成本,提高发电稳定性。显热储热是利用储热材料温度上升或者下降来存储或释放热量的,显热储热原理简单、技术成熟,应用广泛。本文选用蜂窝陶瓷作为高温固体显热储热的材料,蜂窝陶瓷具有耐高温、比表面积大、流动阻力和热惯性低等优点。首先搭建蜂窝陶瓷蓄热系统的试验系统,进行储热性能试验研究;在试验的基础上,提出了改进的蜂窝陶瓷传热模型,利用数值模拟分析不同参数(包括换热系数等随温度变化的参数)对于储热效果的影响,综合考虑各参数的影响设计能够长期稳定运行的储热系统。
2.模型
图1是显热储热模型的示意图。高温空气从蜂窝陶瓷的圆形通道流入,与陶瓷材料的壁面进行热传导与对流换热。空气流动的方向为x,垂直方向为y。
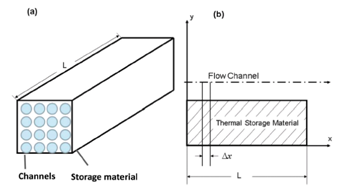
图1 :储热模型(a 储热模块 b储热单元横截面)
对模型做出以下几点假设:
(1)固体材料的热传导在Y方向无穷大,即横截面上温度分布均匀(壁厚很薄)
(2)固体材料的初始温度分布均匀
(3)y方向上每个通道的边界绝热(y方向没有热损失)
(4)储热和放热过程空气的质量流量恒定
第一,壁厚很薄,忽略y方向上的温差,y方向壁面的对流热阻为导热热阻的几十倍(壁厚很薄)符合经典豪森理论和努赛尔理论;第二,默认当储热系统工作时初始温度分布均匀;第三,每个通道在模型中为一个独立的单元,边界绝热;第四,当空气泵稳定工作时,在充放能阶段入口空气质量流量稳定。
根据相关资料,一维能量方程如下:
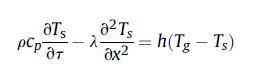
固体材料:
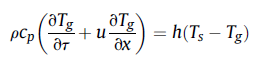
空气:
空气的雷诺数小于2200,因此为层流状态,传热关联式为:
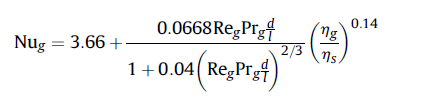
边界条件如下:
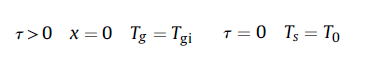
储热系统的热效率定义为冷空气在放热过程吸收的热量与储热过程热空气放热量之比。
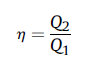
3.实验装置
实验装置的示意图如图2所示。
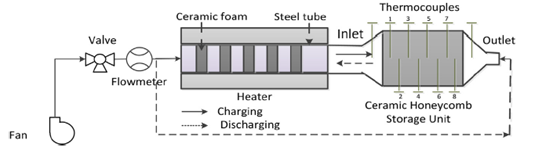
图2 :实验装置示意图
空气流量由流量计测得,并经过充满多孔泡沫结构的陶瓷的不锈钢管的电炉进行加热,热空气进入顺序排列有蜂窝陶瓷的储热模块,加热蜂窝陶瓷的过程称之为储热过程。在放热过程,冷空气从相反方向流入以带走储热阶段存储的热量。
具体试验步骤如下:
(1)打开电炉,设臵电炉的升温程序。
(2)连接电脑和数据采集仪,开始进行数据采集。
(3)在电炉升温至设定温度时,打开风机向管式炉内鼓入冷空气,调节阀门开度,控制空气流量,通过转子流量计测量流量的大小。
(4)观察数据采集仪采集的数据,当蓄热系统内温度基本达到稳定时,关闭电炉,整个加热时间约为2小时。
(5)改变空气流动方向,反向向蓄热系统内通入冷空气并调节气体流量,当蓄热系统出口空气温度下降到较低温度时,停止试验。
(6)保存数据,关闭电源。
储热材料周围包裹着绝热材料以减少热损,8个热电偶在两侧以5cm的间距对称布置,蜂窝陶瓷的热物理参数如表1所示。,碳化硅基质的蜂窝陶瓷具有最小热膨胀系数及最大的热导率,但使用温度最低;而氧化铝与氧化硅的热物性较为相似。由于价格低廉且热物性良好,多采用氧化铝基质的蜂窝陶瓷。
表1:典型蜂窝陶瓷的热物理参数

4.实验与讨论
4.1实验结果与讨论
图3表示整个试验过程中蓄热系统内的温度分布,其中编号1~8代表沿着蓄热期空气流动方向依次间隔布臵的8个热电偶。在本试验中,由于温度限制,定义300℃为蓄热有效温度,由图可知,整个蓄热期为2小时,而放热期约为0.5小时。在蓄热期内,进入蓄热系统的空气在管式炉内迅速升温,蓄热系统的温度随着热空气的进入而随之升温。整个蓄热系统内的温度分层明显,出口段的温度最低。在蓄热1小时后,蓄热系统整体温度达~300°C,升温速度逐渐变缓。在蓄热2小时后,进入蓄热系统的热空气温度基本达到准稳态,整个蓄热系统内的温差基本在50℃左右。在放热期,冷空气(~30°C)由相反方向进入蓄热系统,蓄热系统的温度随着冷空气的进入下降剧烈。放热期的蓄热系统进口端(i=8)在约6 分钟后温度即下降至300℃以下;而出口端(i=1)的温度变化相对缓和。在30分钟后整个蓄热系统的温度下降到300℃。
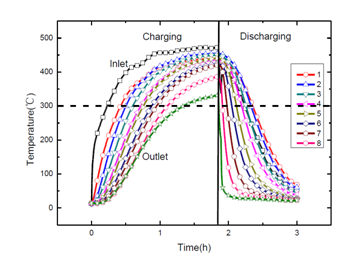
图3: 储热系统内各点温度随时间变化曲线
图4表示不同蓄热时间后整个蓄热系统沿轴向的温度分布曲线。由图可知,蓄热系统的进口段温度最先上升,之后将热量通过热传导方式向后传递,出口部分的温度上升最为缓慢。蓄热系统内的温度分层明显。随着蓄热时间,蓄热系统进口部分的升温幅度逐渐减少,在蓄热期结束后,蓄热系统内的温度分布均匀,整体温差为50℃左右,出口段的温度由于受到外部环境的影响温度最低。
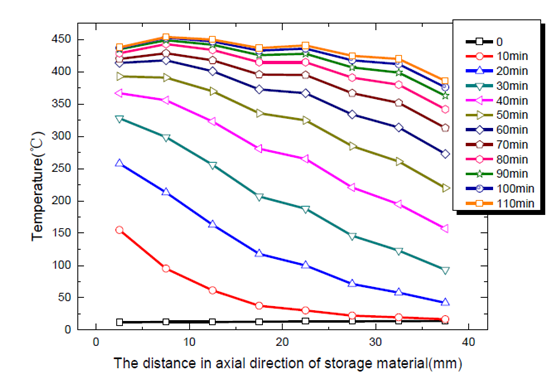
图4 :不同储热期储热系统整体的温度分布曲线
图5对比了蓄热材料不同壁厚、不同空气流量对于蓄热系统出口空气温度的影响。由图可知,在相同流量时,蓄热材料壁厚对于蓄热期的出口空气温度影响不大,而对于放热期,壁厚越大,蓄热材料能蓄积的热量越大,在放热期出口空气温度变化较为缓和,降温较慢。当其他参数一致而仅增大流量时,蓄热期内的出口空气温度升温较快,但放热期的温度变化也较为剧烈,降温较快。
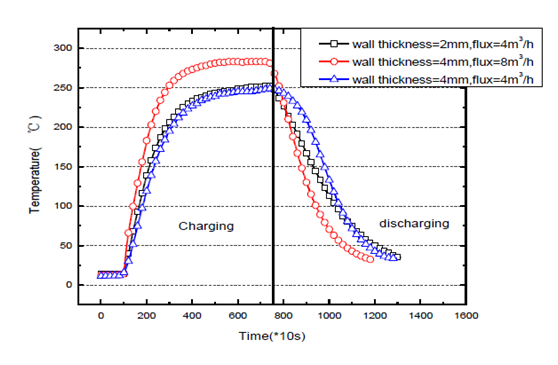
图5: 储热材料壁厚及空气流量对出口空气温度的影响
4.2模型与实验结果对比
综合来看,模拟结果与试验值吻合性较好。在蓄热期,进口部分的模拟值与试验结果偏差较小;沿着x 方向,两者之间的差异逐渐增大。而在蓄热期结束时,整个蓄热系统内的模拟结果与试验值的误差在5%以内,模型较为准确。在放热期,模拟结果与试验值的差异较蓄热期明显,模拟值较之试验值下降较慢,说明在实际试验过程中,放热速率超过预期。在放热期结束时,蓄热系统靠近出口部分(x=12.5cm)两者温差约为20℃,而在出口处模拟值高于试验值约70℃,这可能是由于空气直接排出蓄热系统受到周围环境影响温度较低。
导致模拟结果与试验值的差异的原因有:(1)文中采用的换热系数计算公式是一个经验公式,这可能与蜂窝陶瓷内部的换热并不十分一致;(2)实际换热过程中固体蓄热材料y方向上有热传导的发生,而在模型中做了忽略;(3)蜂窝陶瓷蓄热体内的每个通道内的流动可能并不完全一样;(4)整个蓄热系统对外界有热损失。
当假设换热系数为常数时,根据空气初始状态计算的气固对流换热为32.4 W/(m2 K) ;而换热系数随着温度变化,它的范围为32.4~43.5 W/(m2 K)。
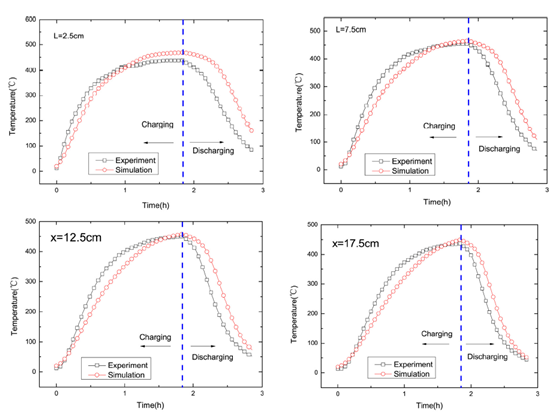
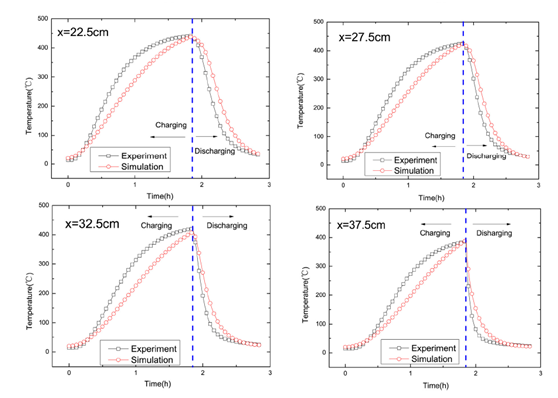
图6: 模拟和实验结果的对比
5模型预测
基于验证后的数值模型,下面将讨论各参数对于蓄热系统热性能的影响,包括蜂窝陶瓷内单个流道的直径(0.003~0.01 m),壁厚(0.001~0.005 m),蓄热材料的热导率(1~5 W/(m•K)),容积热容(1500~4500kJ/(m3 K))及流量等。假设蓄热系统的初始温度为600℃,蓄热期热空气进口温度1000℃,蓄热时间10小时;放热期冷空气进口温度为300℃,放热时间6小时。
5.1热物性参数
图7表示了3种不同蓄热材料热导率(1,3,5W/(m•K))对于蓄热系统出口空气温度的影响。由图可知,热导率对于蓄热期出口空气温度影响较大,而在放热期差异不明显。随着蓄热材料热导率的增加,蓄热期的出口空气温度较低,而在放热期出口空气温度下降较为缓和且最终稳定在较高值。在6小时放热结束后,三者温差约为80℃。对于三种热导率的蓄热材料,放热期内出口空气温度均在1.1小时左右即下降到600℃左右,表明蓄热材料的热导率对于蓄热系统放热期的影响并不显著。
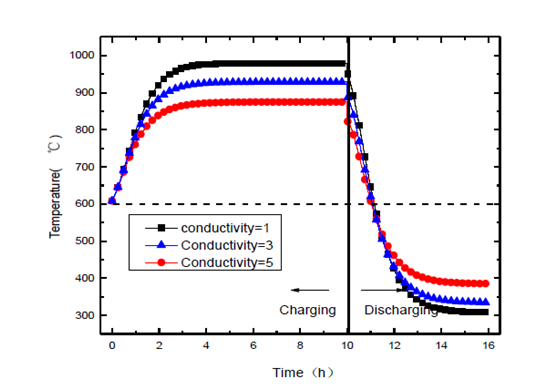
图7 :储热材料热导率对空气出口温度的影响
定义容积热容量为蓄热材料密度和比热容的乘积,这是衡量显热蓄热系统蓄热能力的一个重要指标。图8表示了蓄热材料不同的容积热容量对于出口空气温度的影响。由图可知,容积热容对于蓄热系统出口空气温度的影响较为显著。随着容积热容的增大,蓄热期内出口空气温度上升速度较为缓慢,由于蓄热时间充足,蓄热期结束时三种容积热容下的空气出口温度最终趋向一致;放热期的出口空气温度随着容积热容的增大而下降较慢,且下降幅度较小。当容积热容量为4500 kJ/(kgm3)时,放热期出口空气温度在3.5 小时左右下降到600℃;而当容积热容量为1500 kJ/(kgm3)时,放热期出口空气温度在1.2 小时左右即下降到600℃。
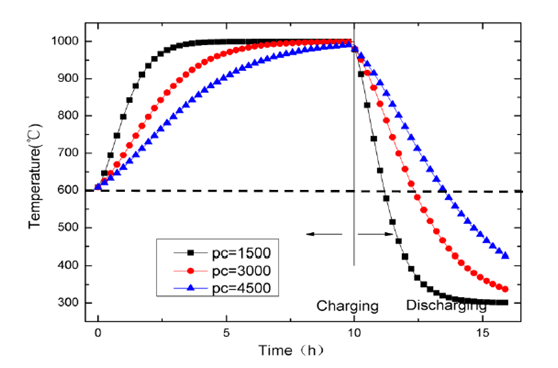
图8: 储热材料体热容对空气出口温度的影响
5.2几何参数
图9a表示了蜂窝陶瓷蓄热体内单个通道的流通直径对于空气出口温度的影响。由图可知,流通直径对于蓄热系统出口空气温度的影响较为显著。在蓄热期内,随着直径的增大,出口空气温度上升较快且最终能稳定在一个较高温度值;放热期的出口空气温度随着直径的增大下降剧烈且快速。当通道直径为0.01m 时,出口空气温度在4 小时蓄热后达到980℃左右并保持稳定,放热期出口空气温度在1.1 小时左右就下降到600℃;当通道直径为0.003m 时,出口空气温度在10 小时蓄热期内升温缓慢且最终仅达到730℃左右,放热期出口空气温度在6 小时内由~880℃下降到~600℃。这说明随着流通直径的增大,换热面积随之增大,气固之间的换热更为显著。图9b表示了蜂窝陶瓷蓄热体内单个通道的壁厚对于出口空气温度的影响。由图可知,蓄热材料的壁厚对于蓄热系统出口空气温度的影响较为显著。随着壁厚的增大,在蓄/放热期内出口空气温度的变化都较为缓和,温度差值较小。当壁厚为0.001m 时,放热期出口空气温度在1.1 小时左右就下降到600℃;当壁厚为0.003m时,放热期出口空气温度在3 小时后才降至600℃;当壁厚为0.005m 时,放热期出口空气温度在5 小时后才会降至600℃。这说明随着壁厚的增大,蓄热材料能储存更多的热量,能支持更长时间的有效放热期。
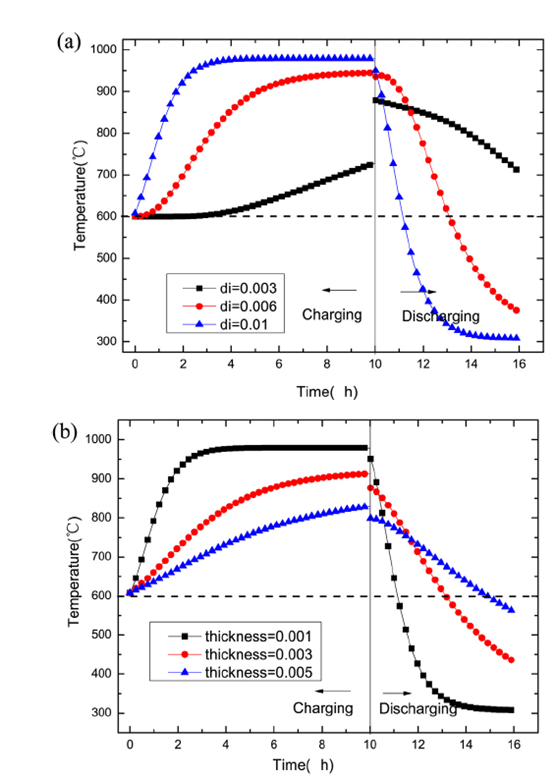
图9 :蜂窝陶瓷储热体几何参数对空气出口温度的影响(a流通直径\b壁厚)
5.3空气流量
图10 表示了空气流量对于空气出口温度的影响。由图可知,空气流量对于蓄热系统出口空气温度的影响不太显著。随着流量的增大,在蓄/放热期内出口空气温度的变化都较为快速且剧烈。当流量为27 kg/h 时,放热期出口空气温度在20 分钟左右就下降到600℃;当流量为9 kg/h 时,放热期出口空气温度在1.2 小时后降至600℃。
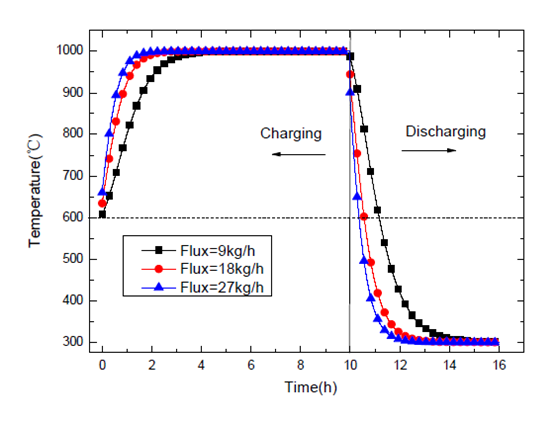
图10 空气流量对空气出口温度的影响
5.4不同放热过程的模拟结果
基于上述的分析,对蓄热系统进行优化设计,结果如图11所示。图11表示了不同参数下对应的放热时间。其中4h 曲线表示蓄热系统出口空气温度在放热期内快速下降且在放热4 小时后温度即下降到600℃。如果仅在蓄热期内增加空气流量而放热期内流量不变,则蓄热期内蓄热系统能蓄积更多的热量,但对放热期的空气温度变化没有显著影响。当通道直径减少或者壁厚增加时,温度变化相对缓和,且有效放热时间(出口空气温度>600℃)可达8 小时。当同时调整蜂窝陶瓷蓄热体的几何参数和空气流量时,出口空气温度在蓄热期内上升缓慢,在8 小时放热期内温度由980℃下降至790℃,有效放热时间可进一步延长;此时蓄热系统的热效率可达90%。这表明当综合考虑蓄热系统的各项参数对蓄热性能的影响并合理设计各项参数时,可以获得长期稳定运行的高温蓄热系统。
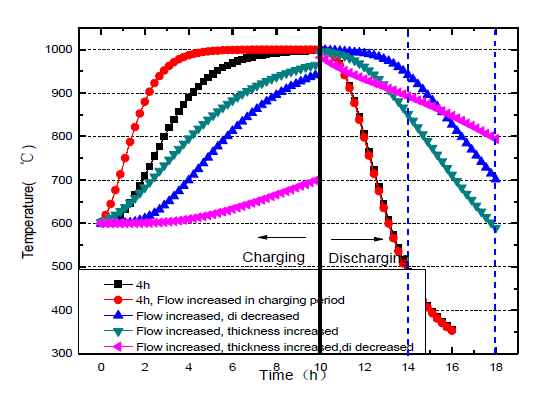
图11 :不同放热时期的温度变化曲线
6.结论
基于蜂窝陶瓷蓄热试验研究,提出了一种改进的数值模型,其中考虑传热系数与空气温度的依变关系。并通过试验验证了模型的准确性。在试验中,蓄热2小时的热量可提供约30分钟的有效放热时间,蓄热系统热效率约为66%。模拟结果和试验值的吻合性较好,在蓄热期结束时,两者偏差在5%以内。而在放热期,两者偏差逐渐明显,出口附近温差约为20℃。
蓄热材料的热导率对于蓄热期出口空气温度影响较明显,随着蓄热材料热导率的增加,蓄热期的出口空气温度较低,而在放热期出口空气温度下降较为缓和且最终稳定在一较高值。蓄热材料的热导率对于蓄热系统放热时间的影响不显著。蓄热系统的储热能力随着容积热容的增大而增大。当容积热容量为4500 kJ/(kgm3)时,放热期出口空气温度在3.5小时左右下降到600℃;而当容积热容量为1500 kJ/(kgm3)时,放热期出口空气温度在1.2小时左右即下降到600℃。当通道直径减少或者壁厚增加时,温度变化相对缓和,且有效放热时间(出口空气温度>600℃)可达8小时。当同时优化蜂窝陶瓷蓄热体的几何参数和空气流量时,出口空气温度在蓄热期内上升缓慢,在8小时放热期内温度由980℃下降至790℃,有效放热时间可进一步延长;此时蓄热系统的热效率可达90%。这表明当综合考虑蓄热系统的各项参数对蓄热性能的影响并合理设计各项参数时,可以获得长期稳定运行且高效的高温蓄热系统。进一步讨论了蓄热系统的稳定性与长期运行的可行性。
参考文献:
Zhongyang Luo, Cheng Wang, Gang Xiao*,MingjiangNi, Kefa Cen. Simulation and experimental study on honeycomb-ceramic thermalenergy storage for solar thermal systems. Applied Thermal Engineering, 2014,73(1): 620-626.


