回热器作为斯特林发动机三大换热部件之一,其换热性能的优劣对发动机整体的功率和效率有着巨大影响。本文介绍了一种应用空隙尺度模拟研究回热器换热特性的方法,分析了不同参数下回热器在振荡流下的瞬态和循环平均换热规律,发现工质在振荡流的加速与减速期间内的加热及冷却过程的换热特性存在较大差异。在此基础上,提出了加热及冷却过程的Nu-Re关联式:Nu=3.56+0.36Re0.66和Nu=17.67+0.37Re0.64,通过实验对比数值模拟结果,误差在7%以内。
1 背景介绍
在当前传统化石能源日益枯竭、环境污染日益严重的背景之下,因为资源丰富、清洁环保等优点,太阳能光热发电领域受到了越来越多研究者的关注。太阳能热发电技术主要分为以下四类:槽式聚光、塔式聚光、碟式聚光斯特林和菲涅尔式聚光发电系统。相比其他三种系统,采用点聚光的碟式系统具有更高的能量转换效率、占地面积小以及对水的需求几乎为零等显著特点,既可以建立10-1000 kW的分布式能源系统,也便于组建1-1000 MW的大型电站,其核心技术之一就是斯特林发动机。
斯特林发动机由加热器、膨胀腔、回热器、冷却器和压缩腔五部分组成,如图 1所示。当工质气体吸热膨胀后,高温气流从热端(加热器和膨胀腔)经由回热器流向冷端(冷却器和压缩腔),回热器储存大部分气体显热;当工质冷却压缩后,低温气流再经由回热器从冷端返回热端,回热器将储存的热量释放给低温气流,完成回热。良好的回热性能可以大幅降低加热器和冷却器的工作负荷,提高发动机的功率和效率。
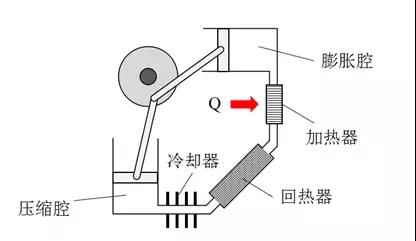
图 1 斯特林发动机示意图
金属丝网,作为如今斯特林发动机中最常用的回热器填料,是一种典型的多孔介质部件,具有极其复杂的孔隙结构。由于丝网内部空间狭小,结构复杂,不利于测量仪器的安装布置,通过实验法获取的数据有限,需要借助数值模拟方法进行研究。对于多孔介质的模拟,除了最常用的表征体元(Representative Elementary Volume, REV)方法外,还有孔隙(Pore)方法。孔隙方法选择部分多孔介质作为研究对象,探究其固体骨架与周围流体间的流动与换热规律,能够直观了解多孔介质内部的流动和换热情况,对理解多孔介质内部流体的宏观输运参数及机理很有帮助。
2 数值模型
选取丝网局部区域作为研究对象,丝网堆叠方式为错列布置,如图2所示。针对100目丝网进行研究,截取的丝网横截面积为0.58 mm2,丝网层数为5层,整体长度L为1 mm,其他具体几何参数如表1所示。

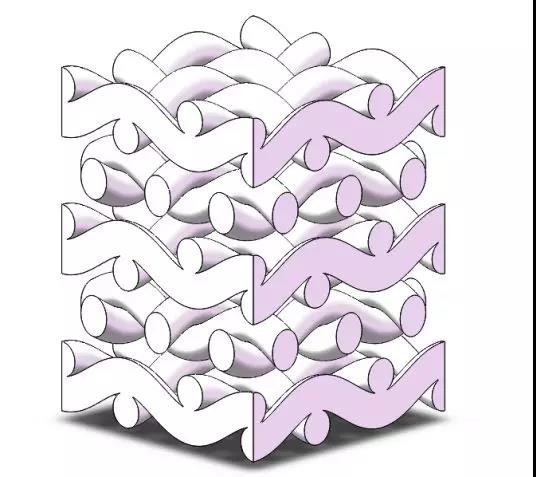
图2 丝网空隙尺度模型
图3展示了完整的计算区域,为避免工质流出丝网后形成尾涡影响计算结果,丝网前后各留了一段长度为丝网1.5倍(1.5 mm)的流道作为缓冲区,同时,选取热端和冷端作为参数监测面。
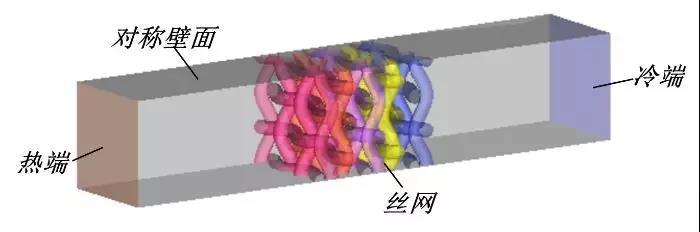
图3 计算区域示意图
网格采用四面体非结构化网格,其中丝网周边部分网格加密,网格质量良好,经过了网格无关性的验证。边界条件设置如表2所示,热端和冷端轮流作为流道入口和出口,每隔半个周期对调进行换向。

选取空气作为工作介质,其物性参数(密度、粘度、比热容、导热率等)随温度变化而变化,相关参数通过REFPROP软件查询并拟合后输入FLUENT中。
丝网与工质气体之间对流换热量Q满足如下关系式:

3 结果分析
针对上文构建的模型,采用二阶迎风格式离散控制方程以及k-ε湍流模型进行计算。选取空气作为工作介质,压力为3 MPa,不同工况下冷端温度恒定为300 K,热端温度、工质速度峰值及变换频率如表3所示。

监控各片丝网的体平均温度,当与前一周期的差值小于1%时,认为工况达到热平衡,并选取热平衡后的单个周期进行分析。按照公式和计算相应的Re数、Nu数等,分析回热器丝网换热特性,并拟合得到相应关联式。
3.1 瞬态换热特性分析
图4(a)是9 m/s-700 K-10 Hz工况下Re数随时间步长变化图,图4(b)是该工况下的瞬态Nu-Re关系图,这里把热平衡后回热器固体加热升温的半个周期称为加热过程,冷却降温的半个周期称为冷却过程。
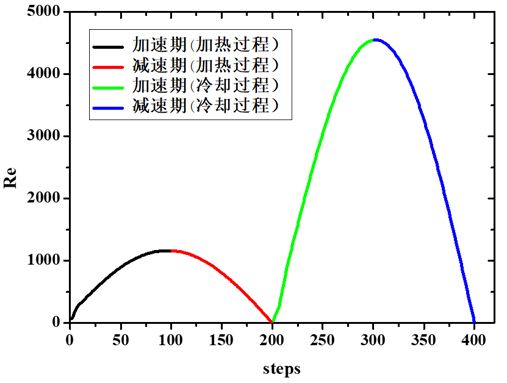
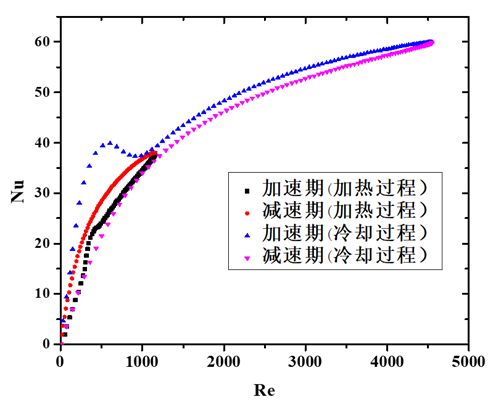
图4 9 m/s-700 K-10 Hz工况的Re-step和Nu-Re瞬态关系图
图5所示为不同工况的瞬态Nu-Re关系曲线,从图中可以发现,同一工况下,加热及冷却过程的Nu-Re曲线不同,长度存在差异,但变化趋势一致。这是由于加热过程中气体的平均温度高于冷却过程,导致气体的密度小,粘度大,因而Re数较小。图5(a)展示了不同入口速度的瞬态Nu-Re曲线,冷却过程的最大Re数比加热过程高266%~302%。图5(b)展示了不同热端温度的瞬态Nu-Re曲线,冷却过程的最大Re数比加热过程高133%~474%;不同曲线的冷却过程最大Re数基本一致,加热过程最大Re数不同,热端温度越高,加热过程的最大Re数越小。可见,热端温度影响加热过程的Re数,冷却过程的Re数受冷端温度影响。
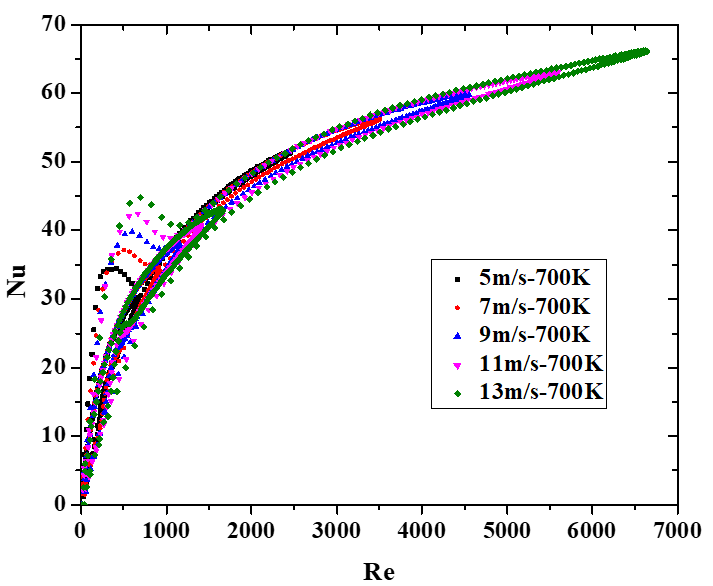
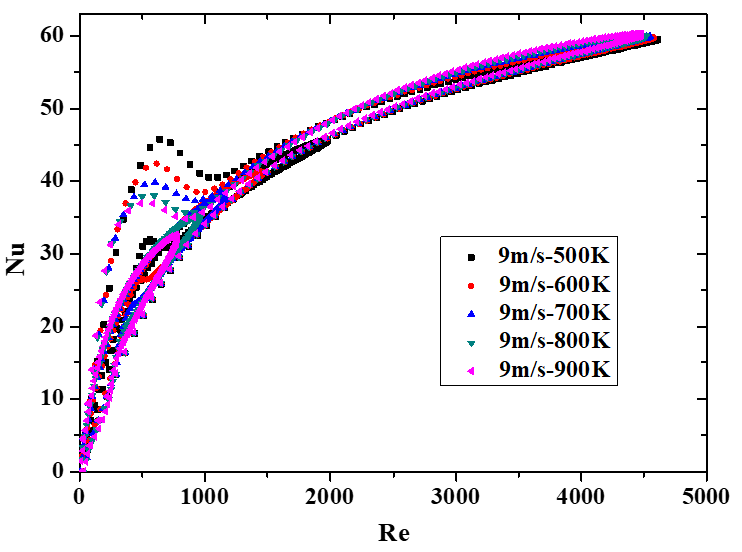
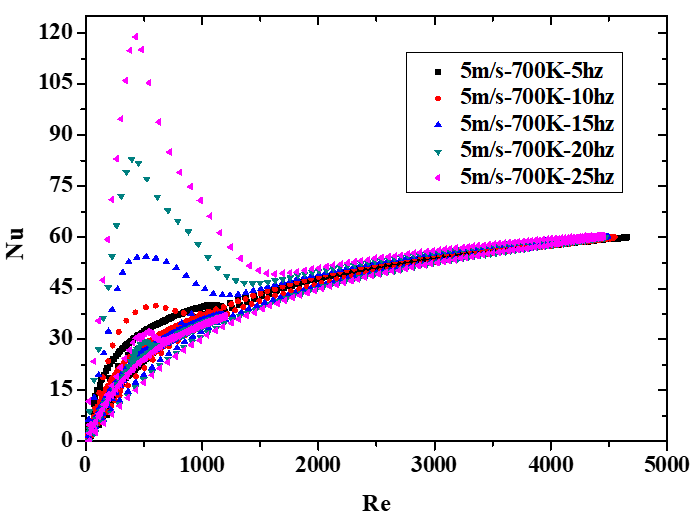
图5 不同速度、热端温度、频率下的瞬态Nu-Re关系图
振荡流下,工质速度呈正弦变化,存在加速与减速期。Isshiki等通过实验研究振荡流阻力特性时,发现加速与减速期的阻力系数曲线存在差别。观察图5,发现加速与减速期的Nu-Re曲线没有完全重合,存在一定差别。加热过程中,加速与减速期的百分比偏差较大,最大差别为14.6%。图6所示是9 m/s-700 K-10 Hz工况下加速与减速期(加热过程)的云图对比,图中两个时间节点的雷诺数相近。明显可以看出,加速期(左边)时流场的平均速度和温度较减速期(右边)偏小。加速期的气体的温度较低,因而密度大,粘度小,同时速度较小,对应的换热系数h和Nu数较小,导致加速期曲线位于减速期曲线下方;反之,冷却过程加速期温度较高,所以加速期曲线位于减速期曲线上方。
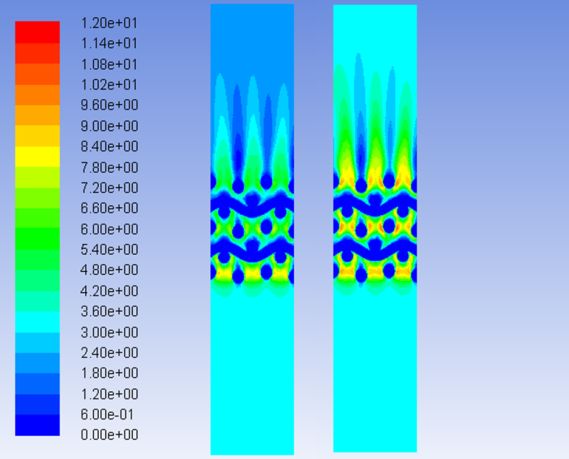
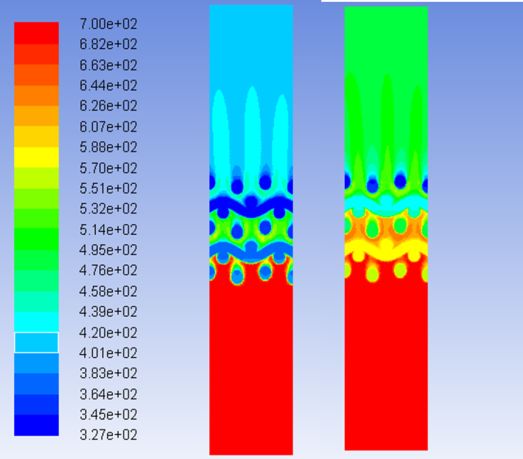
图6 加速期和减速期云图对比
在加热和冷却过程的起始阶段,Nu数都会存在部分较大值,使得Nu-Re曲线存在阶段性“凸起”,这个现象在冷却过程中尤其明显。Sun和Yuan在实验中也发现了该现象,认为是由于此时的气固温差较小导致的。Yuan还发现随着频率增加,凸起部分的峰值和占比也随之增加,这与图5(c)中显示的模拟结果一致。本文认为主要是由于换向时刻流动紊乱,同时存在向热端和冷端的流动,加强了对流换热强度,使得Nu数存在较大值。
3.2 循环平均换热特性分析
在振荡流工况下,工质的速度场、温度场及压力场都处于周期性变化过程中。将数据经过循环平均处理后,能够更为直观地观察到入口速度、温度等变量对换热特性的影响。对各物理量进行算术平均后,根据相应公式计算换热系数h等参数,如图7所示。
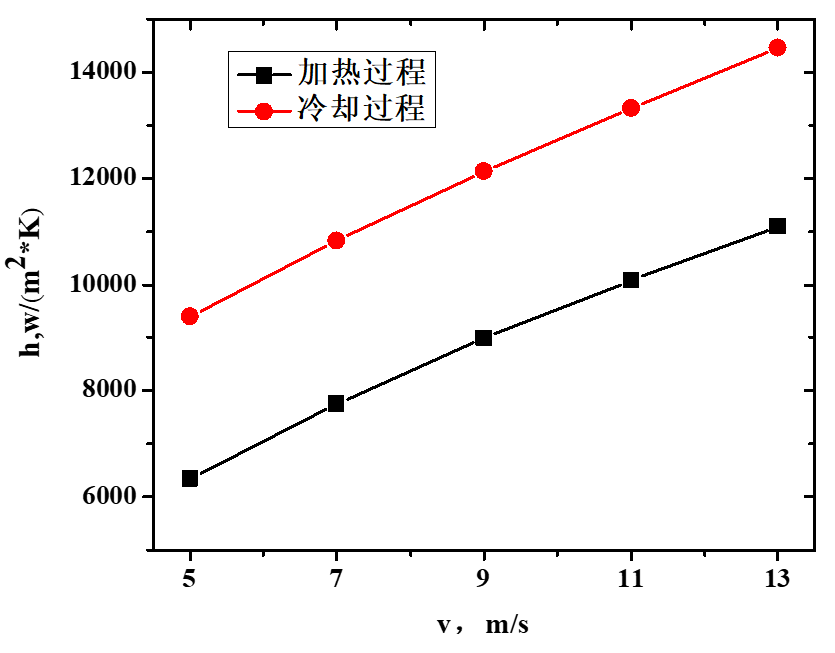
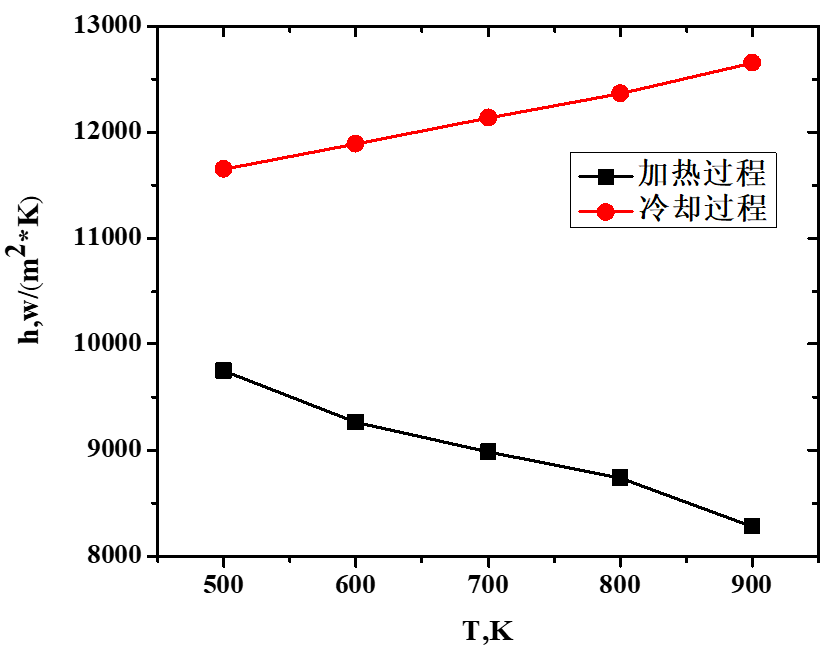
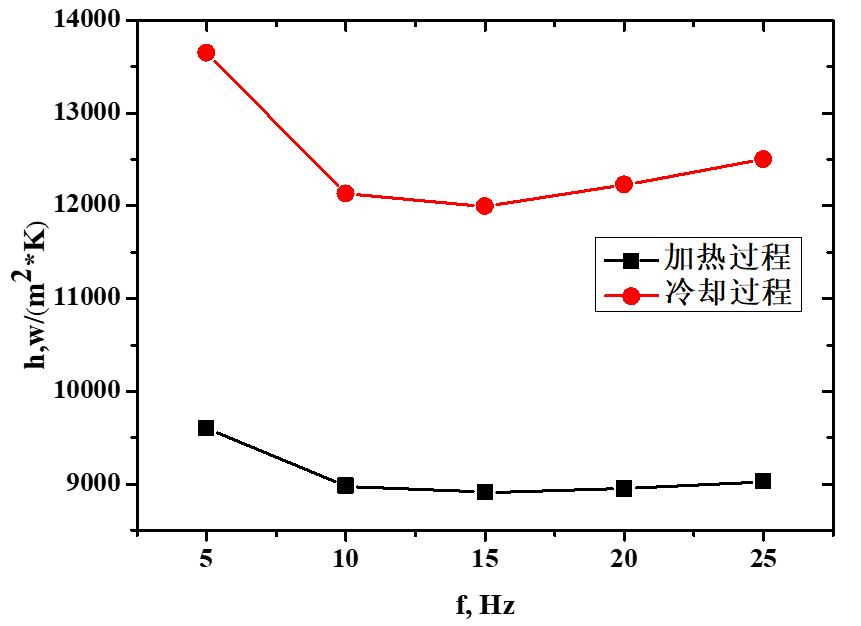
图7 不同速度、温度、频率下换热系数h变化图
如图7所示,冷却过程换热优于加热过程。这是由于在冷却过程中,工质温度低于丝网壁面温度,近壁面的工质会被加热,温度升高,导致热边界层流动紊乱,涡量增大,使得相同工况下,冷却过程的换热系数h大于加热过程。如图7 (a)所示,入口速度越大,对流换热效果越好,换热系数h和Nu数也随之增大。在图7 (b)中,随着温度上升,加热过程和冷却过程的换热系数h的变化趋势不同。加热过程中,随着热端温度提高,入口气体密度减小,气体进出口温差和气固温差变化幅度基本一致,因此换热系数h随着密度下降;而在冷却过程,气体入口温度均为300 K,气体热物性参数基本不变,热端温度的变化影响了初始阶段的丝网温度,热端温度越高,丝网初始温度越高,气固之间的温差较大,换热系数h较大。图7 (c)展示的是不同频率下换热系数h的变化规律,频率较小时,换热所需时间较长,换热过程进行得比较充分,因而平均换热系数h较大。随着频率增加,单个周期的换热时间缩短,换热量减少,但初始阶段扰动剧烈,瞬态换热系数h较大,当频率继续增加时,换向初期的扰动影响变大,循环平均换热系数h略微增大。因此,随频率增加,循环平均换热系数h呈现先减小,再略微增大的趋势。
3.3 换热关联式
在回热器的研究中,Nu数常写成Re数的函数(Pr数近似为0.7),并满足如下通用关联式:
Nu = c1 + c2Rec3
其中,公式中的参数c1、c2及c3一般通过实验确定。表4汇总了部分换热关联式。
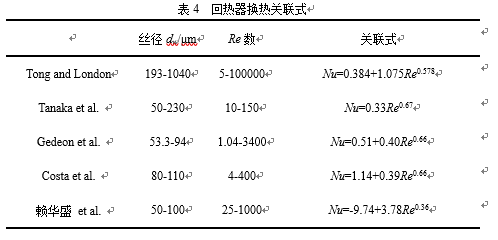
图8展示了加热和冷却过程中的不同数据点,通过软件拟合,得到公式形式的换热关联式:
Nu=3.56+0.36Re0.66
Nu=17.67+0.37Re0.64
对比发现,拟合关联式和Gedeon提出的关联式比较接近,在低雷诺数区间(400-2000),Gedeon关联式与加热过程关联式最大差别为5%;在高雷诺数区间(2000-3400),Gedeon关联式和加热及冷却过程的关联式最大差别小于7%。此外,与文献研究的单向流模拟结果进行了对比,可以看出振荡流曲线位于单向流曲线的上方,在低雷诺数区间差别较小,随着Re数提高,Nu数的差值越来越大,当Re数为2500时,单向流与振荡流加热过程的Nu数差别为20%。由此可见,振荡流的换热效果优于单向流,尤其是在高雷诺数范围。振荡流工况下,加热曲线位于冷却曲线的下方,随着Re数增加,两者的差别减少,当Re数为1000时,冷却过程的Nu数比加热过程高22%;而当Re数为5000时,冷却过程的Nu数仅比加热过程高1%。由于加热曲线和冷却曲线在低雷诺数区间存在较大差异,建议在斯特林循环的高阶分析方法中采取多个换热关联式,以获得更准确的模拟结果。
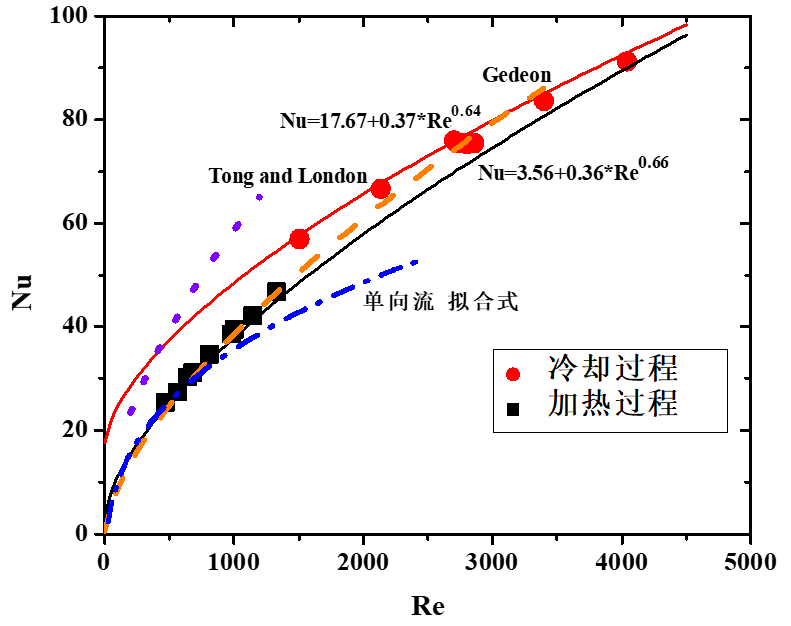
图8 Nu-Re关系图
4 结论
回热器作为斯特林发动机中极其重要的换热部件,因为自身的复杂孔隙结构和振荡流工况,使得研究人员对其内部的换热情况缺乏足够的认识与了解,往往使用相对易得的单向流换热公式代替进行循环分析。本文介绍了孔隙方法研究回热器在振荡流下换热的方法,指出了振荡流的换热效果优于单向流,同时振荡流的加热和冷却过程的换热强度存在差别,并得出了这两个过程的拟合关联式,适用于斯特林分析方法,有助于完善斯特林发动机设计优化方法。
参考文献
1.范皓霆,肖刚,赖华盛,彭浩,倪明江. 斯特林回热器振荡流换热特性模拟研究[J]. 工程热物理学报,2018.(已录用)
(作者:倪明江,肖刚等)


